Write Down The Equation And Transformation Matrix For 3D Rotation About X, Y and Z-Axis
• For 3-D rotation, we need to pick an axis to rotate an object.
• The most common choices are the x-axis, y-axis, and z-axis.
X-Axis Rotation
• The transformation for x-axis is obtain from equation of z-axis rotation by replacing cyclically as shown here:
x -> y -> z -> x
• Rotation about x-axis, we leave x co-ordinate unchanged.
y' = ycosθ - zsinθ
z' = ysinθ + zcosθ
x' = x
• Matrix equation is:
p' = Rx (θ) * p
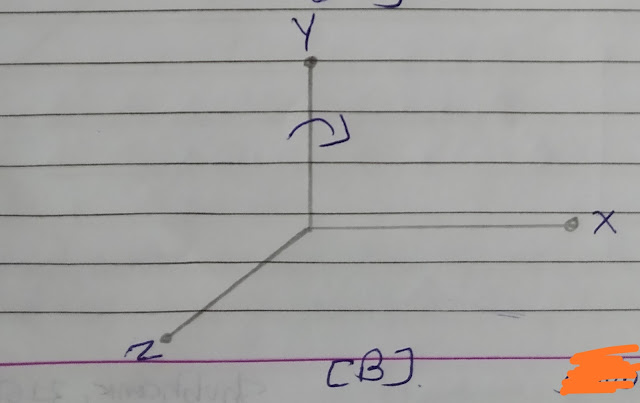
Y-Axis Rotation
• The transformation for y-axis is obtain from equation of x-axis rotation by replacing cyclically as shown here:
x -> y -> z -> x
• Rotation about y-axis, we leave y co-ordinate unchanged.
z' = zcosθ - xsinθ
x' = zsinθ + xcosθ
y' = y
• Matrix equation is:
p' = Ry (θ) * p
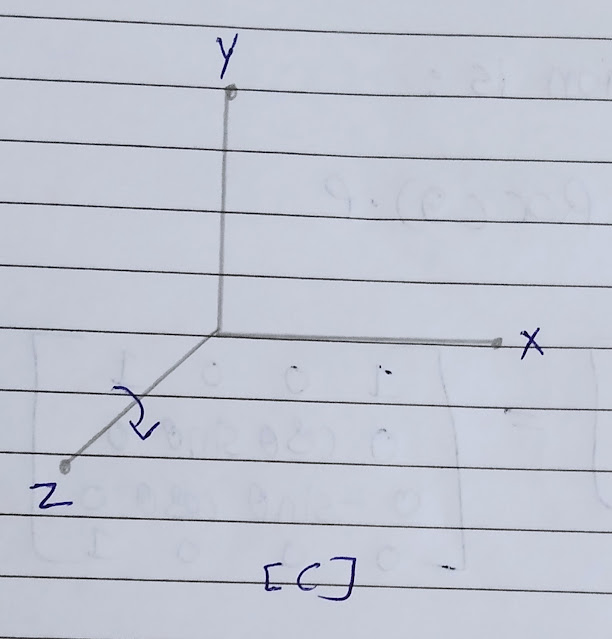
Z-Axis Rotation
• Two-dimension rotation equation can be easily converted into 3-D z-axis rotation equation.
• Rotation about z-axis, we leave z co-ordinate unchanged.
x' = xcosθ - ysinθ
y' = xsinθ + ycosθ
z' = z
• Where, parameter θ specify rotation angle.
• Matrix equation is:
p' = Rz (θ) * p
2-D Viewing Plane In Computer Graphics
Comment your views on this Article :)



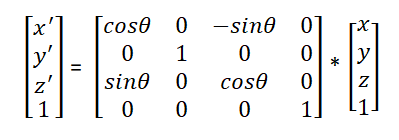





No comments
Comment your views on this article