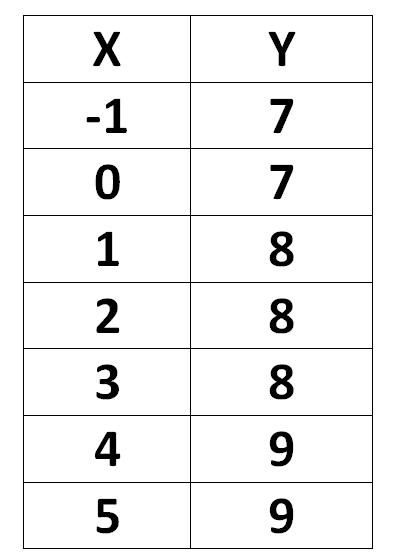
Illustrate Bresenham Algorithm For Calculating The Points For Line Having Endpoints (-1, 7) to (5, 9)
Points -> (-1, 7) to (5, 9)
Bresenham (-1, 7, 5, 9)
{
dx = abs (-1 - 5) = 6
dy = abs (7 - 9) = 2
m = (float) (9 - 7) / (5 - ( - 1)) = 0.33
if (6 >2) then
{
p = 2 * 2 - 6 = -2
twody = 2 * 2 = 4
twodydx = 2 * (2 - 6) = -8
if (-1 > 5) false
else
x = xa = -1
y = ya = 7
xend = xb = 5
putpixel (-1, 7, 3)
while (-1 < 5)
{
x = 0 // x++;
if (-2 < 0) then
p = -2 + 4 // p = p + twody
putpixel (0, 7, 1)
}
while (0 < 5)
{
x = 1 // x++;
if (2 < 0) false
else
if (0 < 0.33 && 0.33 < 1) then
y = 8 // y++;
p = 2 + (-8) = -6 // p = p + twodydx
}
putpixel (1, 8, 2)
}
while (1 < 5)
{
x = 2 // x++;
if (-6 < 0) then
p = -6 + 4 = -2 // p = p + twody
putpixel (2, 8, 4)
}
while (2 < 5)
{
x = 3 // x++;
if (-2 < 0) then
p = -2 + 4 = 2 // p = p + twody
putpixel (3, 8, 1)
}
while (3 < 5)
{
x = 4 // x++;
if (2 < 0) false
else
{
if (0 < 0.33 && 0.33 < 1) then
y = 9 // y++;
p = 2 + (-8) = -6 // p = p + twodydx
}
putpixel (4, 9, 1)
}
while (4 < 5)
{
x = 5 // x++;
if (-6 < 0) then
p = -6 + 4 = -2 // p = p + twody
putpixel (5, 9, 1)
}





No comments
Comment your views on this article